GPU Perf+Segmented Point Clouds

Performance

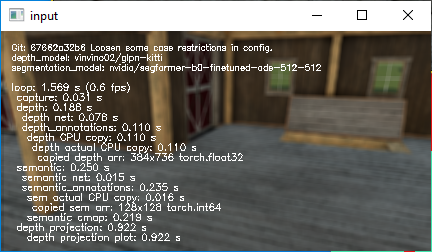
Went through the pipeline and made sure everything stays on the GPU until visualization time. Video here.

A few major contributors to the speed improvements since my first attempts (see this video playlist):

• Use an image capture library that can keep data on GPU.
• At first, I thought I'd have to use PyCuda and some opengl calls to do this myself, but now I think that d3dshot is doing this if you ask for output="pytorch_gpu", or, even better (we need floats for the next step), "pytorch_float_gpu".
• dxcam claims to offer "seamless integration with ... PyTorch", and has more recent releases than d3dshot, but, in practice, d3dshot was faster. 🤷‍♂
• Still, dxcam further claims to be capable of 240 Hz, so maybe I was using it wrong.
• Don't use Huggingface's provided pipelines, which will convert images to NumPy internally to do pre-processing like scaling. Instead, I recreated their preprocessing operations with torch operations on GPU ... as they actually suggest (minus the GPU discussion).
• Use some profiling to see what steps are really the slow ones!

Camera Parameters

I then spent some time playing with camera parameters (focal lengths, sensor center definition, and extrinsic of rotation and translation) to backproject the depth data, colored by semantic segmentation, the camera's frame in physical 3D coordinates. (video)

For my reference, the relevant equations are

$\vec x = [\mathbf{R} | \vec T] \cdot \mathbf{K}^{-1} \cdot [\vec{u}; 1] d$

where

1. $\vec x$ is the camera's 3d position;
2. the extrinsic parameters are
3. $\mathbf{R} = \left[\begin{array}{ccc} c_z c_y,& c_z s_y s_x - s_z c_x, &c_z s_y c_x + s_z s_x \\ s_z c_y,&s_z s_y s_x + c_z c_x,& s_z, s_y, c_x - c_z s_x \\ -s_y,&c_y s_x,&c_y c_x \end{array}\right]$ , the $3\times3$ rotation defined by sines $s_i$ and cosines $c_i$ of the $i=x,y,z$ Euler angles,
4. and $\vec T$, the $3\times 1$ translation of the camera;
5. $\mathbf{K} = \left[\begin{array}{ccc} \ell_u, & 0, & u_0 \\ 0, & \ell_v, & v_0 \\ 0,&0,&1 \end{array}\right]$ is the (intrinsic) camera matrix;
6. $\vec u$ is the $2\times1$ images space coordinates (defined as going from 0 to 1, from top left to bottom right);
7. and $d$ is the scalar depth (this equation is defined per pixel).

So, I can precompute $[\mathbf{R} | \vec T] \cdot \mathbf{K}^{-1} \cdot [\vec{u}; 1]$ and, at runtime, just multiply pointwise by $d$, right?

Unfortunately, I'm a doofus, and I instead wrote

$\hat{\vec{T}} + \hat{\mathbf{R}}^{-1} \cdot \mathbf{K}^{-1} \cdot [\vec{u}; 1] d$

That is, I backproject, unrotate, and then translate instead of backproject, translate, and then rotate.

So, the best I can do is precompute $\hat{\mathbf{R}}^{-1} \cdot \mathbf{K}^{-1} \cdot [\vec{u}; 1]$ for now, until I

• Redefine camera extrinsics so that translation comes before rotation in backprojection.

With this definition, I tried setting up some scenes with visually identifyable geometry so I could twiddle the parameters until they looked sorta right. E.g., the Tesla model X is about 5 meters long, 1.7 high, and 2 wide without mirrors:

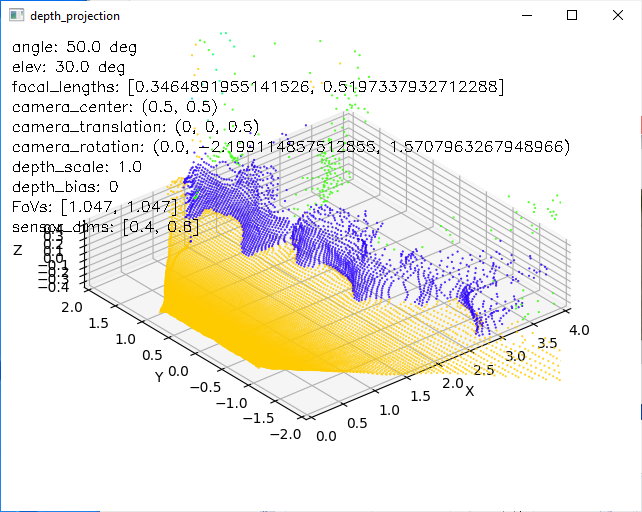
Definitions aside, one thing I found helpful was to realize that there's a relationship

$\ell_i = \frac{\Delta_i}{2 \tan (\alpha_i / 2)}$

between the focal length $\ell_i$ in direction $i=u,v$ and (1) the corresponding sensor dimension $\Delta_i$ and (2) field of view $\alpha_i$. Since $\alpha_i=\pi/3$ is one of the few things I actually do know from the game, I can enter this, and then adjust $\Delta_i$ instead of $\ell_i$, which seems to be less sensitive in hand-tuning.

However, I do think the next step here is to

• Use COLMAP to estimate camera parameters from a few frames, and for a few vehicles like this guy says he did.

instead of eyeballing it. (This needs to be redone per vehicle since each requires a different crop of the whole view to exclude dashboard, since the segmentation models don't reliably detect it.)

However, even at this stage, and even with all the very slow plotting driving the FPS down, the results are good enough ...

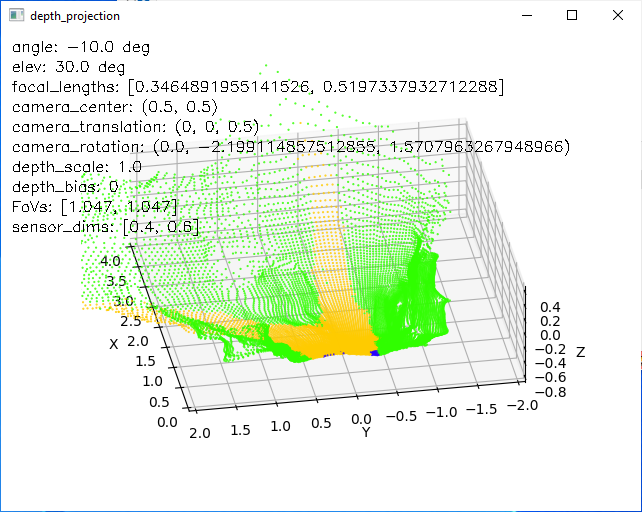
... that I could imagine doing the following with them:

• Set up ROS2 on this machine; maybe in a container.
• Publish as ROS topics these segmented point clouds in some usable format, with suitably backdated timestamps.
• Assign the segmented classes to different bins based on how bad (or good) it would be to drive on/through them.
• Use a Lua mod (see other entries) to
• Publish acceleration and orientation data as an IMU topic
• Maybe publish some sparse ray tracings as ultrasound topics.
• Accept control commands
• Use e.g. RTAB-Map to integrate these.

(I checked all these off since I'm migrating them to the next journal entry [[FS22 2023-05-18]].)

It might also be worth trying to find a monocular depth network that gives better predictions (DPT sounds good -- I might be able to use one trunk network to get both depth and segmentation). Alternatively (and this would take a bunch of time), I could use those sparse raytraces to make my own sparsely-supervised fine-tuning dataset. At the very least, this might help to make the errors less biased (I think the GLPN tends to underestimate).

It could be useful to make use of successive frames, but I can't find any easily available pre-trained nets that do this. This Facebook repo uses single-frame neural depth as the prior for a more conventional SfM method. That might not be too hard to get going, but it seems superficially to be equivalent to just giving the bad point cloud to RTAB-Map with appropriate uncertainties.