Hamiltonian Networks
Use the automatic-differentiation capability of a deep learning framework to make an objective function that includes the partial derivative conditions of a Hamiltonian system.
This was published in Chaos as "On learning Hamiltonian systems from data" with this (long!) abstract:
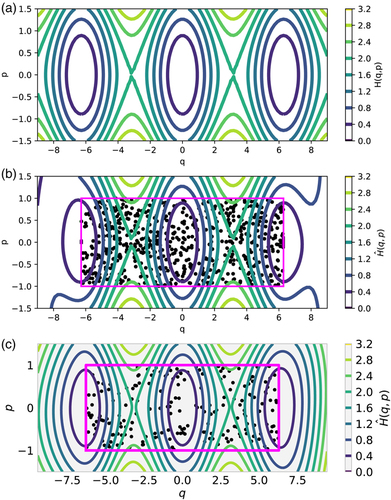
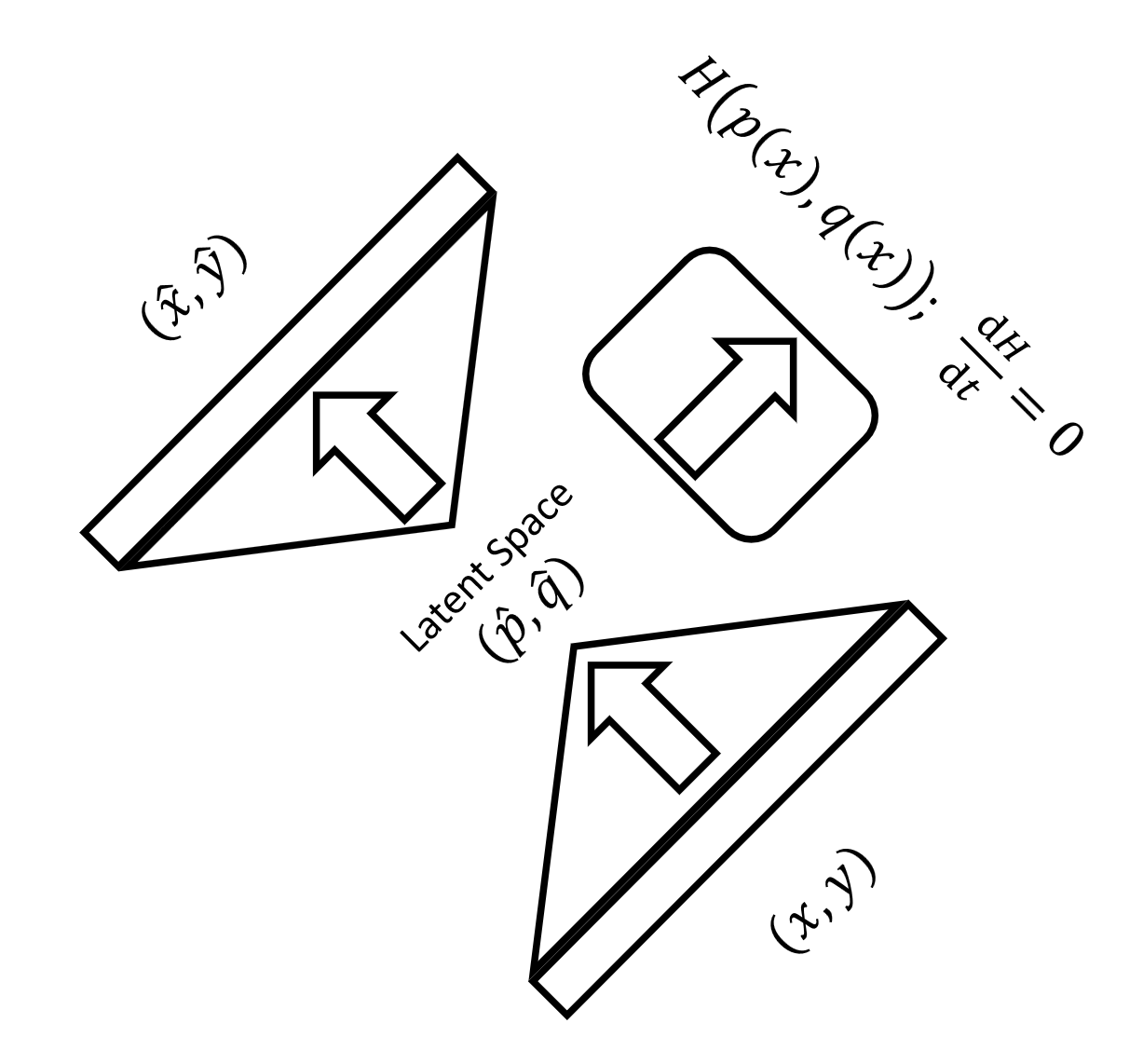
Concise, accurate descriptions of physical systems through their conserved quantities abound in the natural sciences. In data science, however, current research often focuses on regression problems, without routinely incorporating additional assumptions about the system that generated the data. Here, we propose to explore a particular type of underlying structure in the data: Hamiltonian systems, where an energy is conserved. Given a collection of observations of such a Hamiltonian system over time, we extract phase space coordinates and a Hamiltonian function of them that acts as the generator of the system dynamics. The approach employs an autoencoder neural network component to estimate the transformation from observations to the phase space of a Hamiltonian system. An additional neural network component is used to approximate the Hamiltonian function on this constructed space, and the two components are trained jointly. As an alternative approach, we also demonstrate the use of Gaussian processes for the estimation of such a Hamiltonian. After two illustrative examples, we extract an underlying phase space as well as the generating Hamiltonian from a collection of movies of a pendulum. The approach is fully data-driven and does not assume a particular form of the Hamiltonian function.
Neural network-based methods for modeling dynamical systems are again becoming widely used, and methods that explicitly learn the physical laws underlying continuous observations in time constitute a growing subfield. Our work contributes to this thread of research by incorporating additional information into the learned model, namely, the knowledge that the data arise as observations of an underlying Hamiltonian system.
We use machine learning to extract models of systems whose dynamics conserve a particular quantity (the Hamiltonian). We train several neural networks to approximate the total energy function for a pendulum, in both its natural action-angle form and also as seen through several distorting observation functions of increasing complexity. A key component of the approach is the use of automatic differentiation of the neural network in formulating the loss function that is minimized during training.
Our method requires data evaluating the first and second time derivatives of observations across the regions of interest in state space or, alternatively, sufficient information (such as a sequence of delayed measurements) to estimate these. We include examples in which the observation function is nonlinear and high-dimensional.